O Wolfram|Alpha é uma excelente calculadora de derivadas de primeiro, segundo e terceiro grau, derivadas em um ponto, e derivadas parciais. Saiba o que são derivadas e como o Wolfram|Alpha faz para calculá-las.
On-line Calculadora de derivada
Calcule derivadas com o Wolfram|Alpha
Muito mais que uma calculadora de derivada on-line
Learn more about:
Tips for entering queries
Insira sua consulta usando inglês simples. Para evitar consultas ambíguas, lembre-se de usar parênteses quando necessário. Aqui estão alguns exemplos que ilustram como pedir por uma derivada.
Access instant learning tools
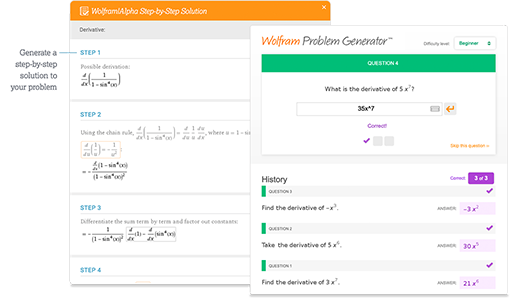
Get immediate feedback and guidance with step-by-step solutions and Wolfram Problem Generator
Learn more about:
O que são derivadas?
A derivada é uma ferramenta importante em cálculo que representa a taxa de variação infinitesimal de uma função em relação a uma de suas variáveis.
Dada a função f x, existem várias formas de demosntar a derivada de f com relação a x. As formas mais comuns são d fd x e f'x. Quando uma derivada é dada n vezes, a notação dn fdxn ou fnx é usada. Estas são chamadas de derivadas de ordem superior. Observe que para as derivadas de segunda ordem, a notação f''x é mais usada.
Em um ponto x = a, a derivada é definida como f'a = limh0f a + h - f hh . Não é garantido que este limite exista, mas se existir, f x é dito que se diferencia em x = a. Geométricamente, f'a é a inclinação da linha tangente de f x at x = a.
Por exemplo, se f x = x3, então f'x = limh0h+x3-x3h = 3x2 e a seguir podemos calcular f''x: f''x = limh03x+h2-3 x2h = 6x. A derivada é uma ferramenta poderosa com várias aplicações. Por exemplo, é utilizada para encontrar extremos locais e globais, pontos de inflexão, resolver problemas de otimização, e descrever o movimento dos objetos.
Como o Wolfram|Alpha calcula derivadas
O Wolfram|Alpha chama a função do Mathematica D, que usa uma tabela de identidades muito maior do que as encontradas em livros de cálculo. A função usa regras "reconhecidas" tais como a linearidade de uma derivada, regra de produto, regra de potência, regra de cadeia, etc. Além disso, D usa regras "menos conhecidas" para calcular a derivada de uma grande variedade de funções especiais. Para derivadas de ordem superior, certas regras tais como a regra geral de Leibniz, podem acelerar os cálculos.